Rock Paper Scissors Lizard Spock Game is an extended version of the classical Rock Paper Scissors game first mentioned in the Season 2 of “Big Bang Theory” by Sheldon Cooper.

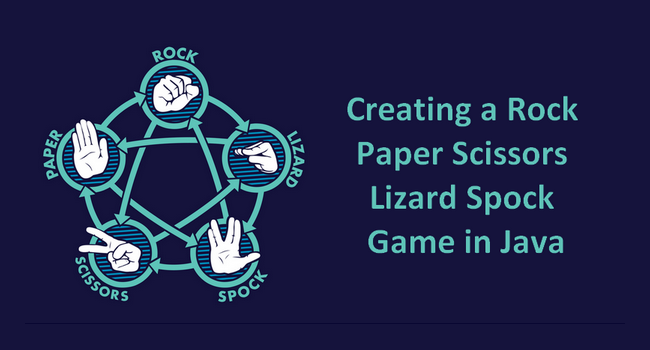
Creating a Rock Paper Scissors Game in Java with a Markov Chain for the AI

As Sheldon Cooper explains, the rules of RPSLS are the following : “Scissors cuts paper, paper covers rock, rock crushes lizard, lizard poisons Spock, Spock smashes scissors, scissors decapitates lizard, lizard eats paper, paper disproves Spock, Spock vaporizes rock, and as it always has, rock crushes scissors.”

In that tutorial, you are going to create your own Rock Paper Scissors Lizard Spock Game in Java with an Artificial Intelligence based on a Markov Chain.

Note that you can also watch this tutorial in video on YouTube :

Representing Items of the Game

First step is to represent items for the Rock Paper Scissors Lizard Spock (RPSLS) Game. For that, we use an enum with five elements :

  • ROCK
  • PAPER
  • SCISSORS
  • LIZARD
  • SPOCK

Each item will have a list of items against whom they lose. Besides, we will use a static block inside en enum declaration to initialize these lists. It gives us the following code for Item enum :

Using a Markov Chain for the AI of the Game

For the Artificial Intelligence (AI) of our RPSLS Game, we are going to use a Markov Chain. It will let us to predict the next move that should be played by the user. Like that, we could react consequently and choosing an item against which the predicted item will lose.

Like said by Wikipedia, A Markov chain is “a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event”.

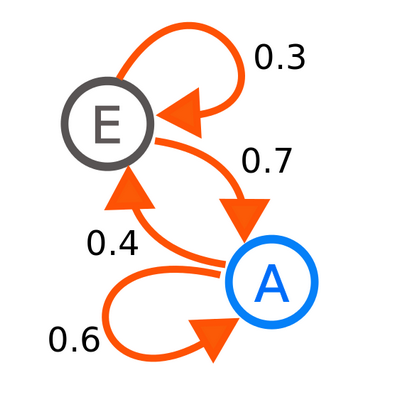
A diagram representing a two-state Markov process, with the states labelled E and A

In the above figure, you can see a diagram representing a two-state Markov process, with the states labelled E and A. Each number represents the probability of the Markov process changing from one state to another state, with the direction indicated by the arrow.

For example, if the Markov process is in state A, then the probability it changes to state E is 0.4, while the probability it remains in state A is 0.6.

In our RPSLS Game, each state will be represented by an Item. During the game, we will store in a Matrix the number of events passing from an item to an other item. Thus, if the user has played ROCK at the previous throw and then, he plays PAPER, we will increment the ROCK to PAPER counter in the matrix.

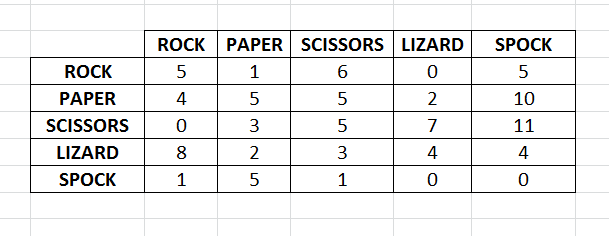
Our Matrix will have the following appearance after several throws :

RPSLS matrix for Markov Chain

Choosing the next move to play

To choose the next move to play for our AI, we will use the Matrix presented previously. We need to know the previous throw made by the user. With that, we choose in the matrix the corresponding line. We iterate on the elements of that line and we choose the item for which the column has the maximum number of events. This is the predicted item for next move of the user.

In our example, imagine the user has thrown a PAPER in the previous throw. By iterating on the associated line, we can predict that the next throw of the user will be SPOCK.

So, we can randomly choose in the list of items against whom SPOCK item loses. It gives us the following code for the nextMove method :

Creating the core of our RPSLS Game

Now, we can create the core of our RPSLS Game. First, we initialize the matrix for our Markov Chain. Then, we use a Scanner to get the user input. We update our matrix by calling the updateMarkovChain method.

In the same time, we call the nextMove method to get the throw choosen by the computer. We check who is the winner of this throwing between user and computer. We display the result of this throwing on the console.

When the user enters STOP, the game is ended. We display some statistics to check the level of our AI for the RPSLS Game. It gives us the following complete code for our game :

Rock Paper Scissors Lizard Spock Game in Action

Now, it’s time to put our RPSLS Game in Action. Once the game is launched, we can play it in the console. After some throws, we can see our AI based on a Markov Chain seems really great :

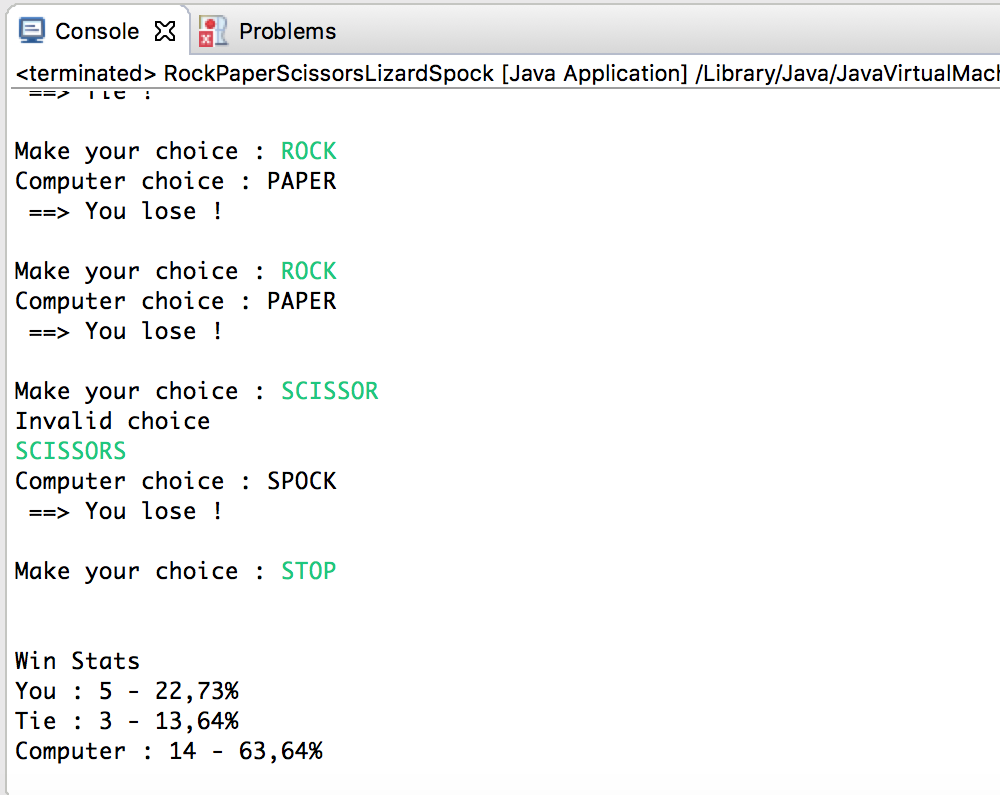
Rock Paper Scissors Lizard Spock Game in Action

Indeed, the statistics after 22 throws are the following :

  • User win : 5/22 (22.7%)
  • Tie : 3/22 (13.6%)
  • Computer win : 14/22 (63.64%)

If you have some comments concerning this tutorial, feel free to use the comments.

This article was originally published here: Creating a Rock Paper Scissors Game in Java with a Markov Chain for the AI.